Linear-logistic function

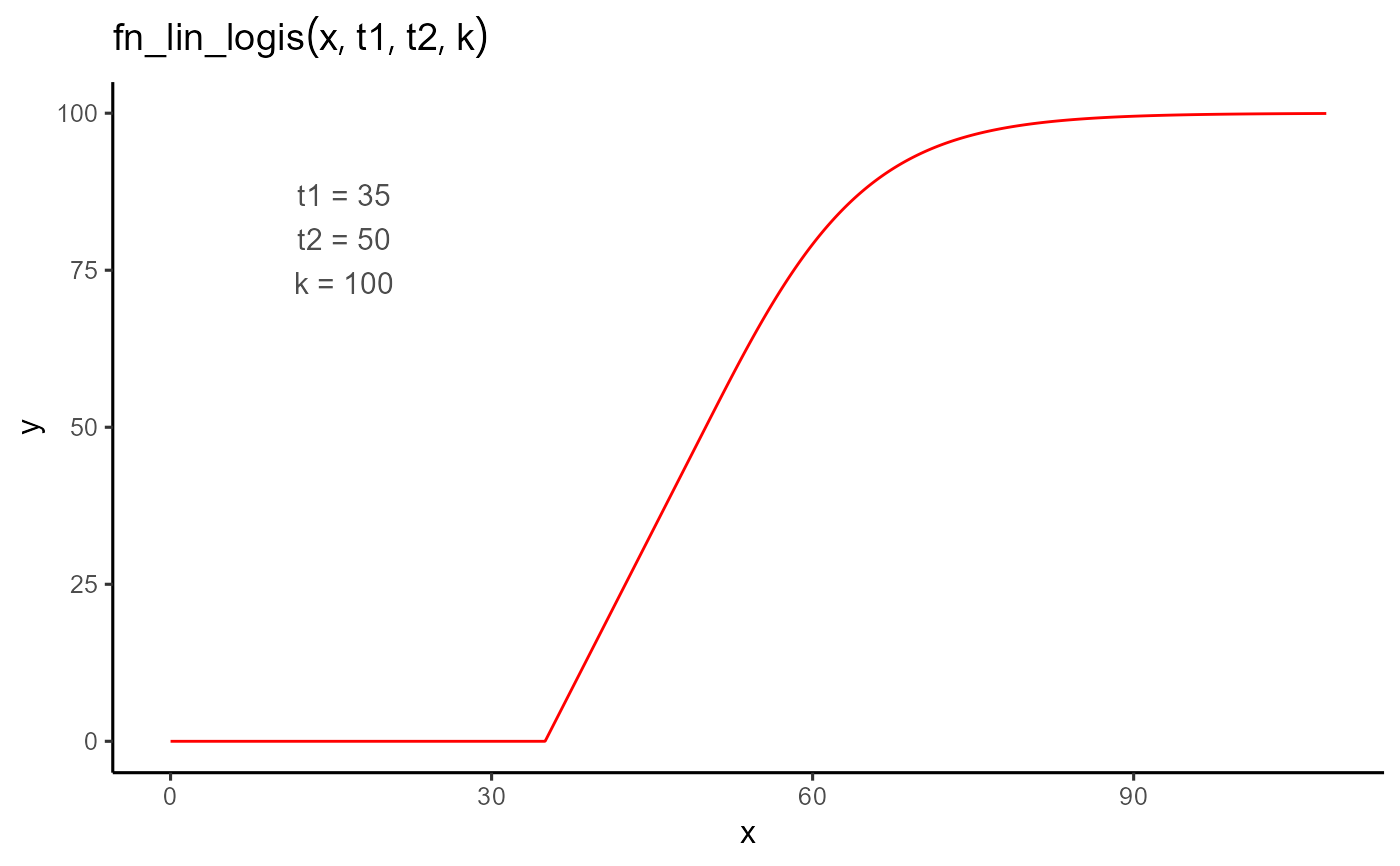
A piecewise function that models an initial linear increase followed by a logistic saturation.

Usage

fn_lin_logis(t, t1, t2, k)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The transition time between the linear and logistic phases. Must be greater than t1.

k

The plateau height. The function transitions toward this value in the logistic phase.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, k) = \begin{cases} 0 & \text{if } t < t_1 \\ \dfrac{k}{2(t_2 - t_1)} \cdot (t - t_1) & \text{if } t_1 \leq t \leq t_2 \\ \dfrac{k}{1 + e^{-2(t - t_2) / (t_2 - t_1)}} & \text{if } t > t_2 \end{cases} $$

The linear segment rises from 0 starting at t1, and the logistic segment begins at t2, smoothly approaching the plateau value k.

Examples

library(flexFitR)
plot_fn(
  fn = "fn_lin_logis",
  params = c(t1 = 35, t2 = 50, k = 100),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)