Linear plateau linear function

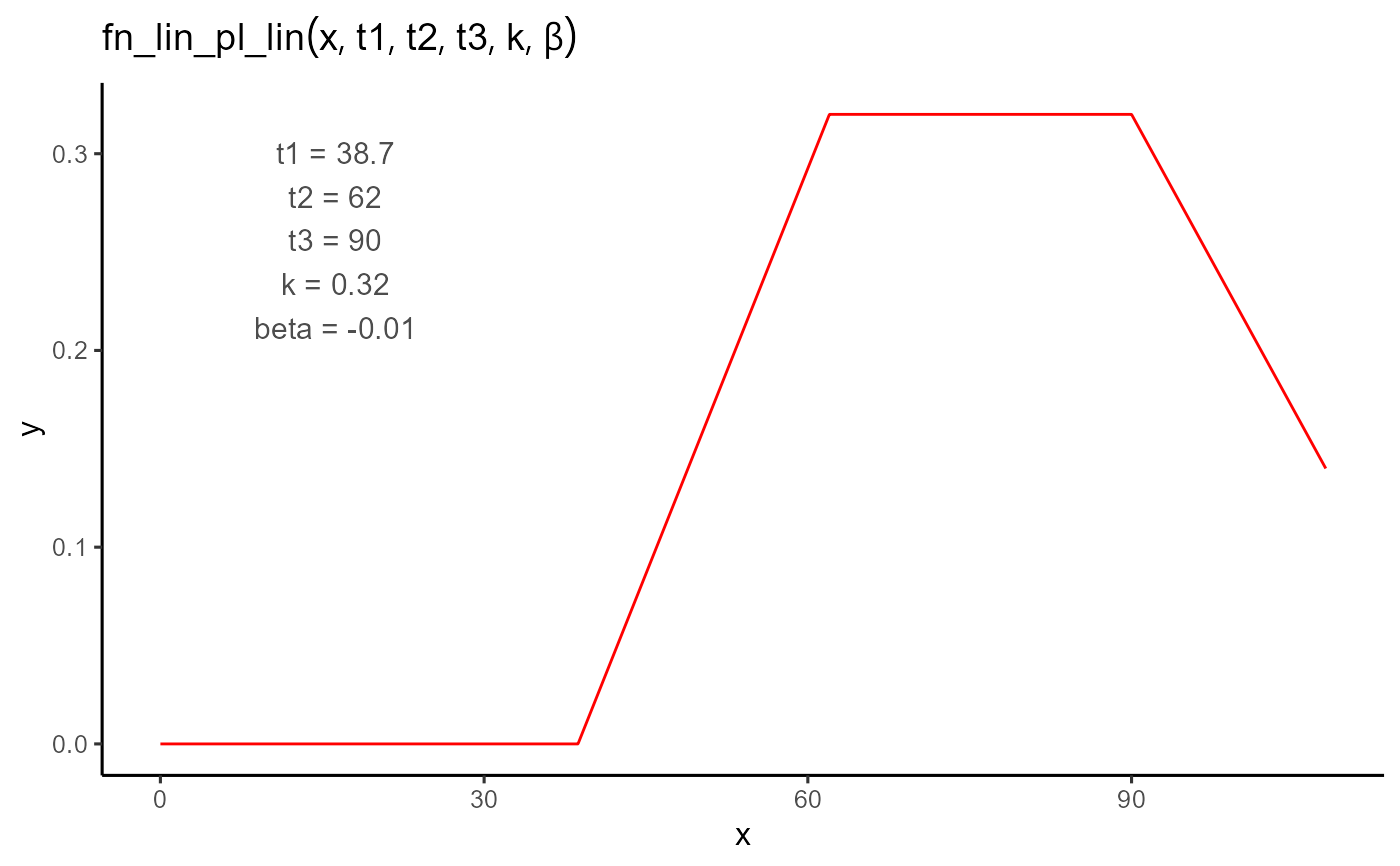
A piecewise function that models an initial linear increase up to a plateau, maintains that plateau for a duration, and then decreases linearly.

Usage

fn_lin_pl_lin(t, t1, t2, t3, k, beta)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The time when the linear growth phase ends and the plateau begins. Must be greater than t1.

t3

The time when the plateau ends and the linear decline begins. Must be greater than t2.

k

The height of the plateau. The first linear phase increases to this value, which remains constant until t3.

beta

The slope of the final linear phase (typically negative), controlling the rate of decline after t3.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, t_3, k, \beta) = \begin{cases} 0 & \text{if } t < t_1 \\ \dfrac{k}{t_2 - t_1} \cdot (t - t_1) & \text{if } t_1 \leq t \leq t_2 \\ k & \text{if } t_2 \leq t \leq t_3 \\ k + \beta \cdot (t - t_3) & \text{if } t > t_3 \end{cases} $$

The function transitions continuously between all three phases but is not differentiable at the transition points t1, t2, and t3.

Examples

library(flexFitR)
plot_fn(
  fn = "fn_lin_pl_lin",
  params = c(t1 = 38.7, t2 = 62, t3 = 90, k = 0.32, beta = -0.01),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)