Linear plateau linear with constrains

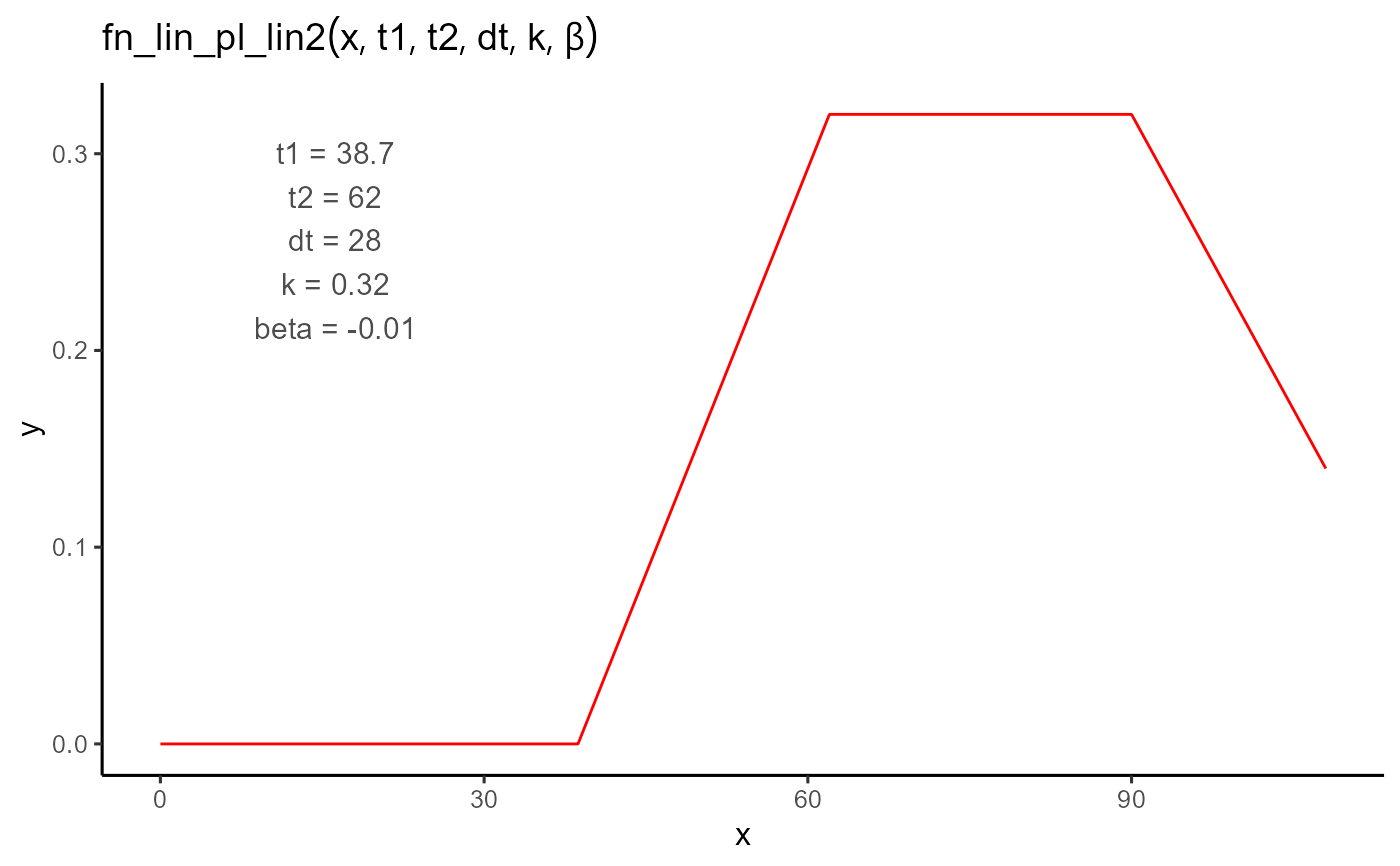
A piecewise function that models an initial linear increase to a plateau, followed by a specified duration of stability, and then a linear decline. This version parameterizes the plateau using its duration rather than an explicit end time, making it convenient for box type of constraints optimizations.

Usage

fn_lin_pl_lin2(t, t1, t2, dt, k, beta)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The time when the linear growth phase ends and the plateau begins. Must be greater than t1.

dt

The duration of the plateau phase. The plateau ends at t2 + dt.

k

The height of the plateau. The linear phase increases to this value, which remains constant for dt units of time.

beta

The slope of the decline phase that begins after the plateau. Typically negative.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, dt, k, \beta) = \begin{cases} 0 & \text{if } t < t_1 \\ \dfrac{k}{t_2 - t_1} \cdot (t - t_1) & \text{if } t_1 \leq t \leq t_2 \\ k & \text{if } t_2 \leq t \leq (t_2 + dt) \\ k + \beta \cdot (t - (t_2 + dt)) & \text{if } t > (t_2 + dt) \end{cases} $$

Examples

library(flexFitR)
plot_fn(
  fn = "fn_lin_pl_lin2",
  params = c(t1 = 38.7, t2 = 62, dt = 28, k = 0.32, beta = -0.01),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)