Linear plateau function

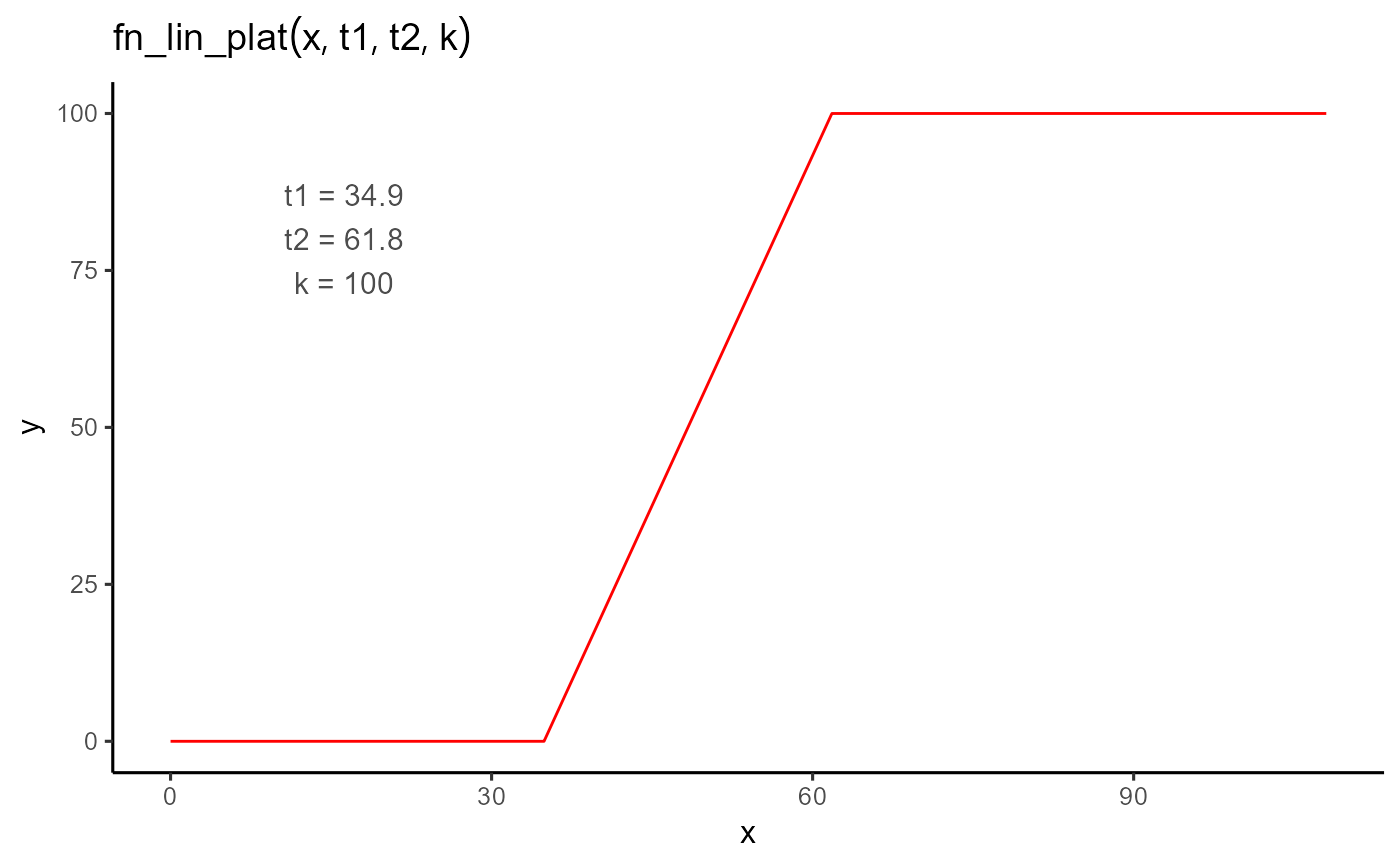
A simple piecewise function that models a linear increase from zero to a plateau. The function rises linearly between two time points and then levels off at a constant value.

Usage

fn_lin_plat(t, t1 = 45, t2 = 80, k = 0.9)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The time at which the plateau begins. Must be greater than t1.

k

The height of the plateau. The function linearly increases from 0 to k between t1 and t2, then remains constant.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, k) = \begin{cases} 0 & \text{if } t < t_1 \\ \dfrac{k}{t_2 - t_1} \cdot (t - t_1) & \text{if } t_1 \leq t \leq t_2 \\ k & \text{if } t > t_2 \end{cases} $$

This function is continuous but not differentiable at t1 and t2 due to the piecewise transitions. It is often used in agronomy and ecology to describe growth until a resource limit or developmental plateau is reached.

Examples

library(flexFitR)
plot_fn(
  fn = "fn_lin_plat",
  params = c(t1 = 34.9, t2 = 61.8, k = 100),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)