Linear–logistic–linear function

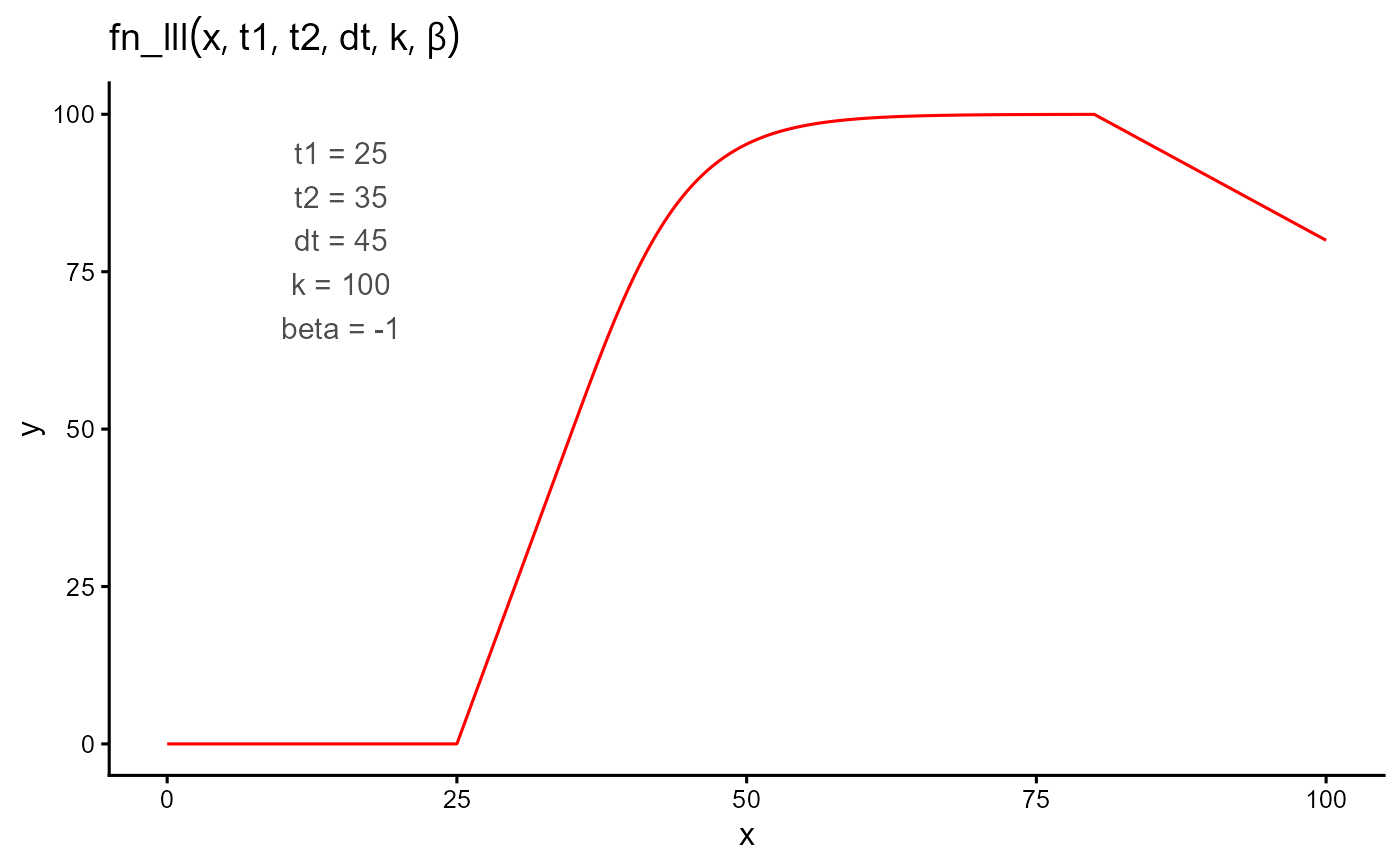
A piecewise function that models (i) an initial linear increase from zero, (ii) a smooth logistic rise toward an upper asymptote, and (iii) a final linear phase.

Usage

fn_lll(t, t1, t2, dt, k, beta = NULL)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than or equal to t1.

t2

The time when the initial linear phase ends and the logistic phase begins. Must be greater than t1.

dt

Duration of the logistic phase. Defines t3 = t2 + dt and must be positive.

k

Upper asymptote (maximum level) of the logistic component.

beta

Slope of the final linear phase after t3 (often negative).

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, dt, k, \beta) = \begin{cases} 0 & \text{if } t \le t_1 \\ \dfrac{k/2}{t_2 - t_1}\,(t - t_1) & \text{if } t_1 < t \le t_2 \\ \dfrac{k}{1 + \exp\left(-2\,\dfrac{t - t_2}{t_2 - t_1}\right)} & \text{if } t_2 < t \le t_3 \\ \dfrac{k}{1 + \exp\left(-2\,\dfrac{t_3 - t_2}{t_2 - t_1}\right)} + \beta\,(t - t_3) & \text{if } t > t_3 \end{cases} $$

where \(t_3 = t_2 + dt\).

The function is continuous at t1, t2, and t3. It is differentiable at t2 by construction (the linear slope matches the logistic derivative at t2). It is not differentiable at t1, and it is generally not differentiable at t3 unless beta matches the logistic derivative at t3.

Examples

library(flexFitR)
plot_fn(
  fn = "fn_lll",
  params = c(t1 = 25, t2 = 35, dt = 45, k = 100, beta = -1),
  interval = c(0, 100),
  n_points = 2000,
  auc_label_size = 3
)