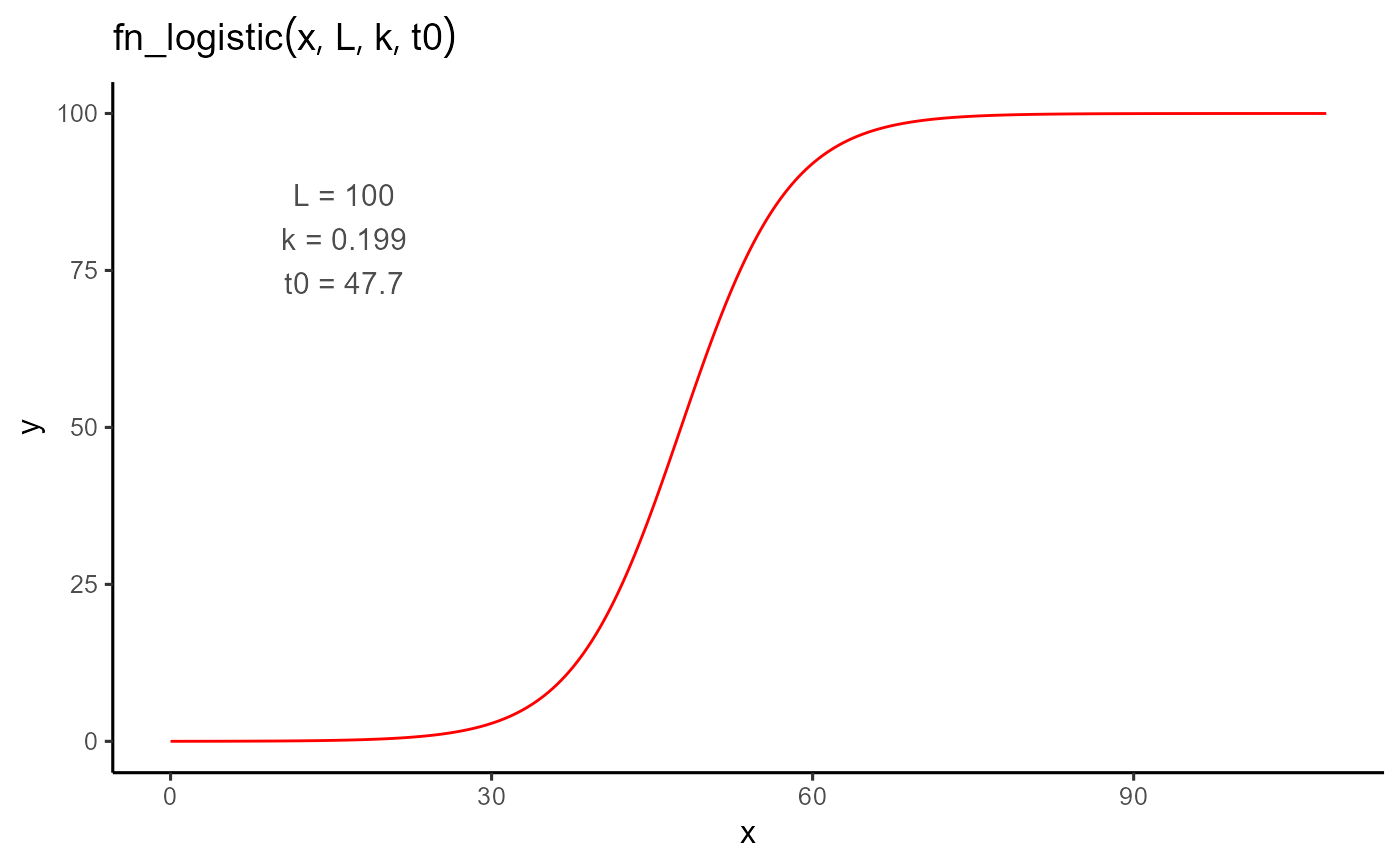
A standard logistic function commonly used to model sigmoidal growth. The
curve rises from near zero to a maximum value k, with inflection point
at t0 and growth rate a.
Arguments
- t
A numeric vector of input values (e.g., time).
- a
The growth rate (steepness of the curve). Higher values lead to a steeper rise.
- t0
The time of the inflection point (midpoint of the transition).
- k
The upper asymptote or plateau (maximum value as t -> Inf).
Value
A numeric vector of the same length as t, representing the logistic function values.
Details
$$
f(t; a, t0, k) = \frac{k}{1 + e^{-a(t - t_0)}}
$$
This is a classic sigmoid (S-shaped) curve that is symmetric around the
inflection point t0.
Examples
library(flexFitR)
plot_fn(
fn = "fn_logistic",
params = c(a = 0.199, t0 = 47.7, k = 100),
interval = c(0, 108),
n_points = 2000
)