Smooth Quadratic-plateau function

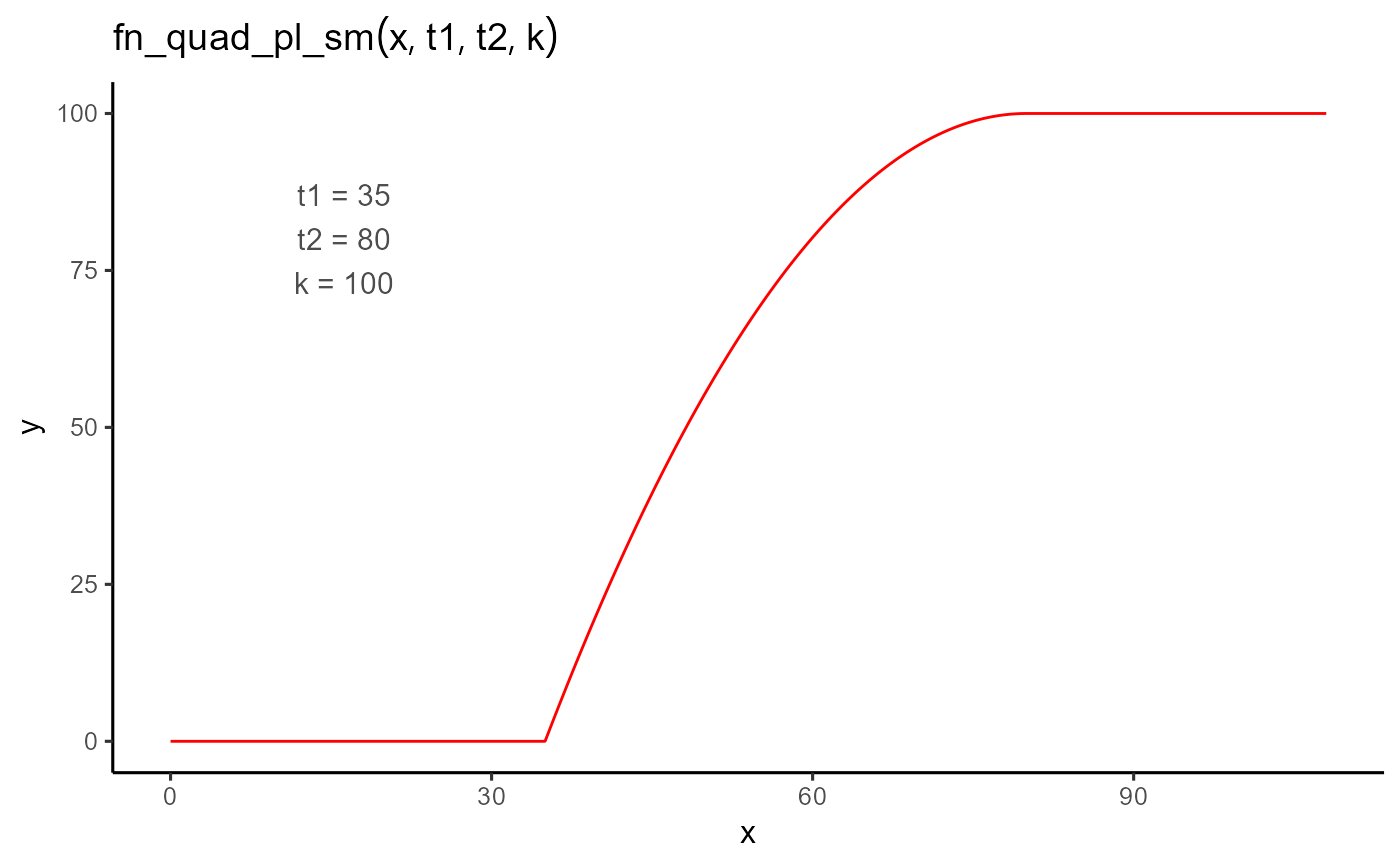
A piecewise function that models a quadratic increase from zero to a plateau value. The function is continuous and differentiable, modeling growth processes with a smooth transition to a maximum response.

Usage

fn_quad_pl_sm(t, t1, t2, k)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The time at which the plateau begins. Must be greater than t1.

k

The plateau height. The function transitions to this constant value at t2.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, k) = \begin{cases} 0 & \text{if } t < t_1 \\ -\dfrac{k}{(t_2 - t_1)^2} (t - t_1)^2 + \dfrac{2k}{t_2 - t_1} (t - t_1) & \text{if } t_1 \leq t \leq t_2 \\ k & \text{if } t > t_2 \end{cases} $$

The coefficients of the quadratic section are chosen such that the curve passes through (t1, 0) and (t2, k) with a continuous first derivative (i.e., smooth transition).

Examples

library(flexFitR)
plot_fn(
  fn = "fn_quad_pl_sm",
  params = c(t1 = 35, t2 = 80, k = 100),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)