Quadratic-plateau function

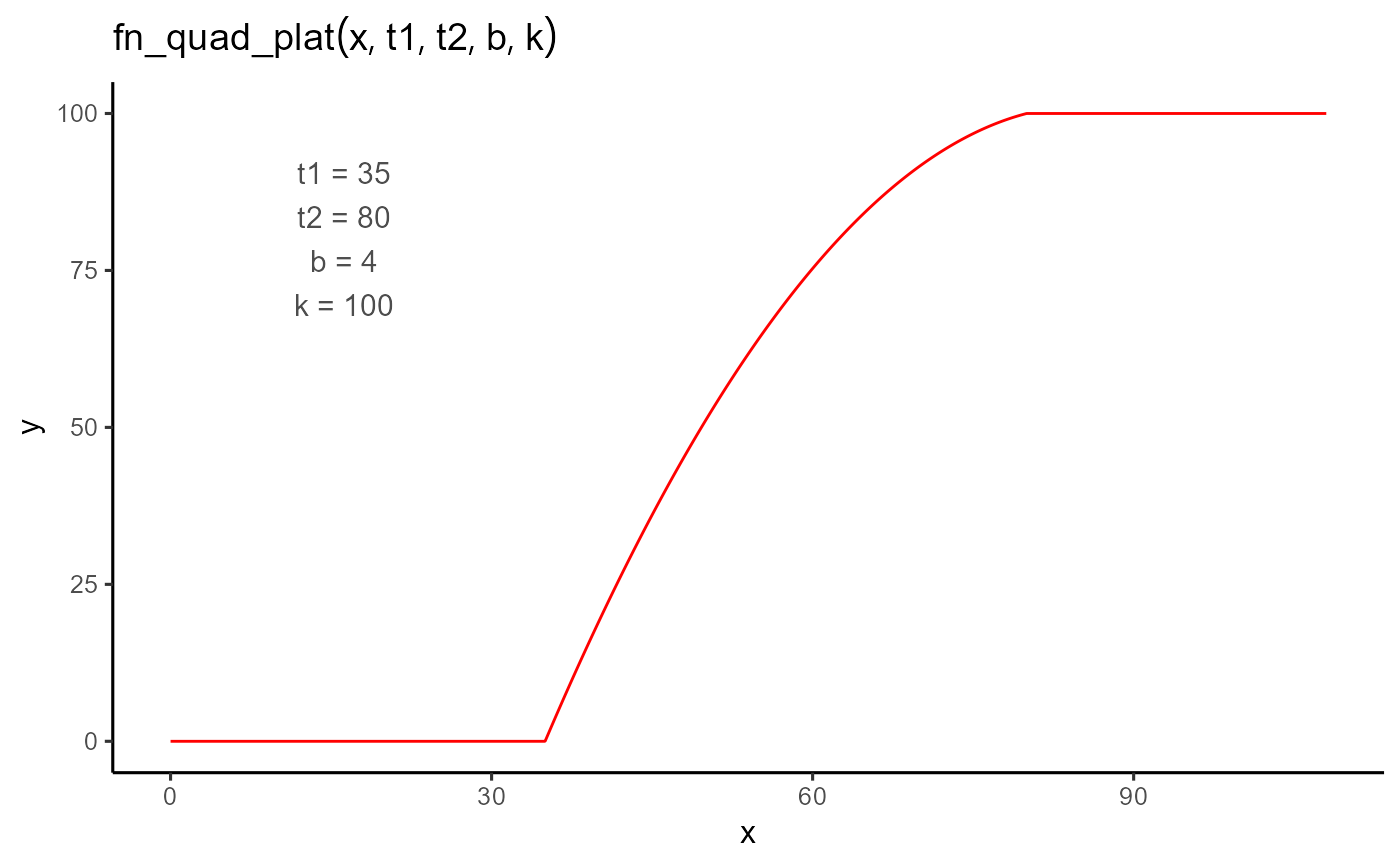
Computes a value based on a quadratic-plateau growth curve.

Usage

fn_quad_plat(t, t1 = 45, t2 = 80, b = 1, k = 100)

Arguments

t

A numeric vector of input values (e.g., time).

t1

The onset time of the response. The function is 0 for all values less than t1.

t2

The time at which the plateau begins. Must be greater than t1.

b

The initial slope of the curve at t1.

k

The plateau height. The function transitions to this constant value at t2.

Value

A numeric vector of the same length as t, representing the function values.

Details

$$ f(t; t_1, t_2, b, k) = \begin{cases} 0 & \text{if } t < t_1 \\ b (t - t_1) + \frac{k - b (t_2 - t_1)}{(t_2 - t_1)^2} (t - t_1)^2 & \text{if } t_1 \leq t \leq t_2 \\ k & \text{if } t > t_2 \end{cases} $$

This function allows the user to specify the initial slope b. The curvature term is automatically calculated so that the function reaches the plateau value k exactly at t2. The transition to the plateau is continuous in value but not necessarily smooth in derivative.

Examples

library(flexFitR)
plot_fn(
  fn = "fn_quad_plat",
  params = c(t1 = 35, t2 = 80, b = 4, k = 100),
  interval = c(0, 108),
  n_points = 2000,
  auc_label_size = 3
)